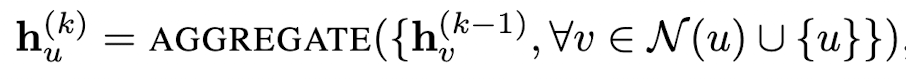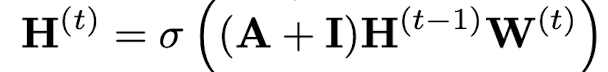Graph Representation Learning Book의 Chapter5을 번역, 요약, 정리했습니다.
이번 장에서는 GNN Graph Neural Networ를 이용한 복잡한 Encoder 모델을 다룹니다. GNN을 이용해 각 노드의 Feature 정보를 포함하면서 그래프 구조를 반영하도록 노드를 임베딩합니다.
Permutaion invariance and equivariance
그래프에 DNN Deep Neural Network를 정의할 때 그래프의 인접행렬을 입렵 데이러도 사용합니다.
가장 간단한 방법으로 인접행렬을 Flatten하여 MLP의 입력 데이터로 사용하는 방법이 있습니다.
[[0, 1, 1],
[1, 0, 0],
[1, 0, 0]] –> [0, 1, 1, 1, 0, 0, 1, 0, 0]
하지만 이렇게 사용할 경우 임의의 노드 순서에 의존적이게 됩니다. 같은 그래프에 대해 노드 A, B, C 순서로 만들어진 인접행렬과 B, C, A 순서로 만들어진 인접행렬ㅇ 서로 다른 입력값으로 인식됩니다. 이 경우 Permutaion Invariant 하지 않다고 합니다.
그래프에 대한 네트워크는 Permutaion Invariant(또는 Equivariant) 해야합니다.
Permutaion Invariant
그래프의 노드 순서에 상관없이 결과가 동일합니다.
\[f(PAP^T) = f(A)\]Permutaion Equivariant
그래프의 노드 순러와 동일하게 결과가 변경됩니다.
\[f(PAP^T) = Pf(A)\]5.1 Neural Message Passing
GNN의 Feature를 정의할 때 Neural Message Passing 형식을 사용합니다. 이때 Message란 노드들 사이에서 교환되고 Neural Network를 이용해 업데이트 되는 벡터입니다.
이번장에서는 입력 그래프 \(G = (V, E)\)를 이용합니다. 노드 Feature는 \(X \in R^{d \times |V|}\), 노드 Embedding은 \(z_u, \forall u \in V\) 를 이용해 표현합니다.
5.1.1 Overview of the Message Passing Framework
GNN의 Message Passing의 반복 과정에서 각 노드 u의 Hidden Embedding \(h_u^{k}\)는 u의 그래프 이웃인 N(u)의 통합 정보를 이용해 업데이트 됩니다.
\[\begin{align} h_u^{(k+1)} &= UPDATE^{(k)}(h_u^{(k)}, AGGREGATE^{(K)}(\{h_v^{(k)}, \forall v \in N(u)\})) \\ &=UPDATE^{(k)}(h_u^{(k)}, m_{N(u)}^{(k)}) \end{align}\]UPDATE와 AGGREGATE는 임의의 함수입니다.
여기서, \(m_{N(u)}^{(k)}\)는 이웃 노드들을 통합하는 “message”라고 합니다. Message Passing 과정에서 각 Layer에 따라 다른 임베딩값을 갖게 됩니다.
Message에 사용되는 Hidden Embedding은 이전 Layer의 값을 이용해 현재 Layer를 업데이트 합니다. 초기 Layer는 \(h_u^{(0)} = x_u\)로 초기화하고, 마지막 층의 결과를 각 노드의 임베딩 벡터로 사용합니다.
\[z_u = h_u^{(K)}\]여기서 \(h_u^{(0)} = x_u\)는 사전에 주어진 각 노드의 정보를 이용할 수 있습니다. 초기에 주어진 특징이 없다면 2장에서 학습한 통계값 또는 One-hot 벡터를 활용합니다.
5.1.2 Motivations and Intuitions
GNN의 Message Passiont 프레임 워크는 straight-forward 합니다. k 번 반복한 Layer는 k-hop 이웃 정보를 반영하게 됩니다.
여기서 반영하는 정보는 그래프의 “구조 정보”와 “노드 특징 정보”로 두가지가 있습니다. 구조 정보로는 k번째 이웃의 Degree 정보들을 포함할 수 있고, “노드 특징 정보”는 모든 이웃 노드의 Feature를 포함할 수 잇습니다.
5.1.3 The Basic GNN
GNN을 구현하기 위해서는 앞에서 정의한 UPDATE와 AGGREGATE를 구체화해야합니다. 가장 단순한 Original GNN 부터 시작해보겠습니다.
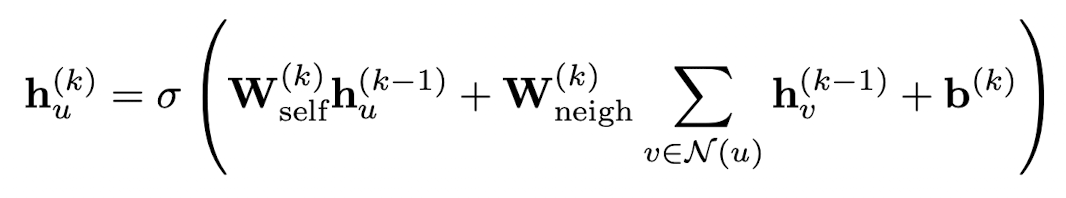
여기서 W는 학습가능한 파라미터 행렬입니다. \(\sigma\)는 tanh와 ReLU와 같은 활성화 함수입니다. bias는 표현식을 간략화 하기 위해 생략되기도 하지만 중요합니다.
UPDATE와 AGGREGATE를 나눠서 표현하면 다음과 같습니다.
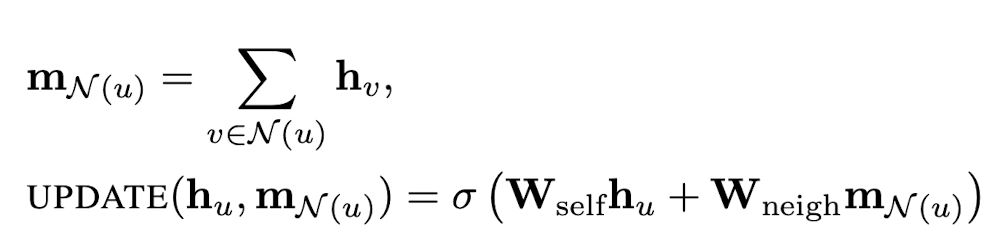
W와 bias는 GNN의 각 Layer마다 다른 Parameter로 사용하거나 공유해서 사용할 수 있습니다.
위 식은 노드 레벨로 GNN을 표현했습니다. 그래프 레벨에서 다음과 같이 Bulk로 표현할 수 있습니다.

5.1.4 Message Passing with Self-loops: self-loop GNN
Neural Message Passiong을 좀 더 간략화하기 위해 self-loop을 추가하고 Update 스텝을 생략할 수 있습니다. Aggregation에서 이웃 노드에 self 노드를 추가합니다. 이 방식은 \(W_{self}\) 와 \(W_{neigh}\) 를 동일한 파라미터로 공유하는 것으로 표현합니다.
업데이트 과정이 생략되어 단순해지는 장점은 있지만, 자신 노드를 구분하지 못함으로 표현력이 약해지고 오버피팅 문제가 생길 수 있습니다.