[CS224W GraphML] 1. GraphML 소개

Graph Representation Learning Book의 Chapter1을 번역, 요약했습니다.

Graph는 점과 점을 연결해 관계를 표현할 수 있습니다. 예를 들어, Social Network에서 사람을 하나의 점 Node로, 두 사람이 친구 관계임을 Edge로 표현할 수 있습니다. 생물학에서는 단백질을 하나의 Node, 단백질 사이의 생물학적 상호관계를 Edge로 표현가능 합니다. Graph는 이렇게 각각의 점들의 속성보다는 점들 사이의 관계를 중심으로 합니다.

최근에 많은 Graph Data가 공개되었고, 이 데이터 내에 존재하는 잠재 정보를 밝혀내기 위한 연구가 진행되고 있습니다. 여러 연구 방법 중 한 가지로 Machine Learning을 이용한 방법을 다룰 예정입니다.

Graph란?

Graph Data는 Node의 집합인 \(N\)와 Edge의 집합인 \(E\)를 이용해 \(G = (N, E)\)로 표현합니다. 하나의 Graph에 속한 Node의 수는 \(|N|\), Edge의 수는 \(|E|\)로 표현합니다. Edge \((u, v) \in E\)는 Node \(u \in N\)에서 Node \(v \in N\)로 연결됐다는 의미를 가집니다.

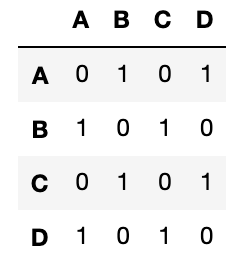
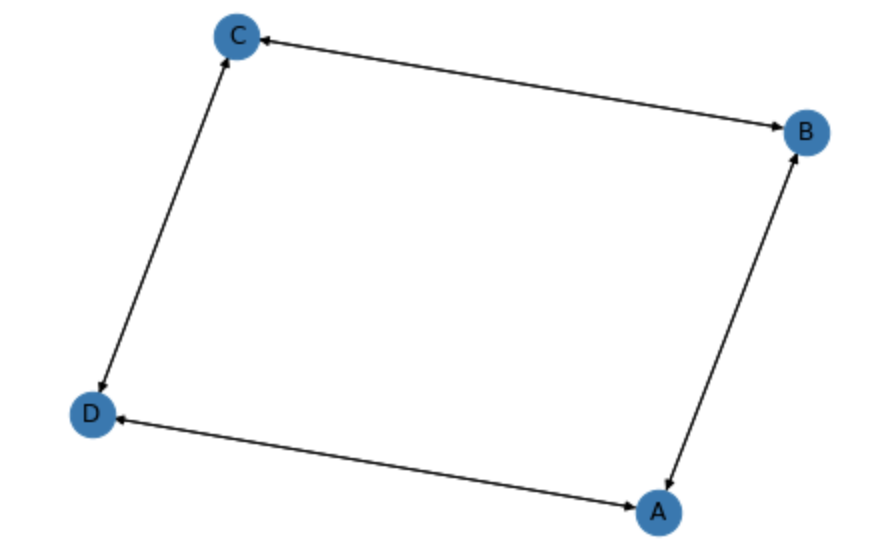
인접행렬 Adjacency Matrix \(A \in R^{|V|\times|V|}\)로 Graph를 표현할 수 있습니다. 모든 Node를 Column과 Row에 나열시키고 연결되어 있으면 1, 연결되지 않은 경우 0으로 표현합니다. 아래 그림처럼 오른쪽 Graph를 왼쪽 행렬과 같이 나타낼 수 있습니다.

Forwarding

Routing

import networkx as nx
import numpy as np

adjacency = np.array([
    [0, 1, 0, 1],
    [1, 0, 1, 0],
    [0, 1, 0, 1],
    [1, 0, 1, 0],
])

labels={0: "A", 1: "B", 2: "C", 3: "D"}

G = nx.DiGraph(adjacency)
nx.draw(G, labels=labels, node_size=500)

Graph의 Edge가 Undirected인 경우 핸열 \(A\)는 대칭 행렬 Symmetric Matrix 입니다. 출발 Node와 도착 Node가 구분된 Directed인 경우 대칭일 필요는 없습니다. Weighted Edge인 경우 행렬값은 0과 1 대신 실수값을 갖습니다. 두 Node의 연결 강도를 표현할 경우 사용합니다.

1.1.1 Multi-Relational Graphs

Undirected, Directed, Weighted Edge로 구분하는 것과 별개로 Edge는 여러 종류를 가질 수 있습니다. 예를 들어, 두가지 약 사이의 부작용 관계를 표현할 때 구토, 설사, 고열 등과 같이 여러 종류의 관게를 표현할 수 있습니다. 이 때 Multi-relational Graphs 라고 합니다. Multi-relational Graphs의 일부로 “Heterogeneous Graph”와 “Multiplex Graph”가 있습니다.

Heterogeneous Graph는 Node가 여러 종류로 나뉘는 경우 입니다. 예를 들어, 단백질에 속하는 Node들, 약에 속하는 Node들, 질병에 속하는 Node들로 Graph가 표현되는 경우 입니다. 이때 약 Node와 질병 Node는 “치료” 관계 Edge를 가지고, 약 Node들 사이에는 부작용 관계를 가질 수 있습니다.

Heterogeneous Graph의 일부로 Multipartite Graph가 있습니다. Multipartite Graph는 Bipartite Graph의 확장입니다. Bipartite Graph는 이분 Graph로 Node들이 두 가지 종류로 나뉘고, 같은 종류의 Node들과는 연결되지 않는 Graph입니다. 예를 들어, “유저가 본 영화” 관계 Graph에서 유저와 영화 사이에만 Edge가 있고 영화와 영화를 연결하거나 유저와 유저를 연결하는 Edge는 없습니다. Node의 종류가 세 가지 이상으로 나뉘는 경우 Multipartite Graph라고 합니다.

Multiplex Graph는 Graph가 여러 Layer로 분해될 수 있는 경우 입니다. 예를 들어, 대중 교통 Graph를 생각해 보겠습니다. 출발지와 목적지가 되는 위치 Node들이 있습니다. 위치 Node들 사이에 버스 또는 지하철 등의 Edge가 있을 수 있습니다. 이때 위치를 연결하는 버스 Edge Layer와 지하철 Edge Layer로 나눌 수 있고, 이 경우 Multiplex Graph라고 합니다.

1.1.2 Feature Information

Graph와 관련된 속성 Attribute / Feature 정보를 가질 수 있습니다. 약 Node라면 주요 성분 등이 속성 정보가 될 수 있습니다. Heterogeneous Graph인 경우 종류가 다른 Node라면 다른 종류의 속성값을 갖을 거라고 예상할 수 있습니다.

1.2 Machine Learning on Graphs

Machine Learning은 어떤 문제를 해결하고 싶은지에 따라 모델이 달라집니다. 기본적으로 입력 데이터에 따라 목표하는 결과를 예측하도록하는 Supervised Task와 데이터의 클러스터를 찾는 것과 같은 Unsupervised Task인 경우로 구분할 수 있습니다.

GraphML도 일반적인 방법과 비슷하지만 Supervised인지 Unsupervised인지 별로 중요하지 않습니다. 주로 Supervised 문제이지만, 전통적인 방법 사이에 경계가 모호합니다.

GraphML의 Task는 크게 4가지 단계로 나눌 수 있습니다.

Node Level
Edge Level
Subgraph/Community Level
Graph Level

이 중 Classic Graph ML Task를 소개하겠습니다.

1.2.1 Node Classification

Node Level의 한 종류인 Node Classification의 목표는 Node의 Label을 예측하는 것입니다. Label은 어떤 종류인지, 카테고리 인지, 속성인지 등이 해당합니다. 예를 들어, 백만 유저를 가진 Social Network가 있을 때 실제 유저가 아닌 Bot을 분류해 내는 문제가 이에 속합니다. 일부 유저 데이터을 Labeling하고 이를 학습해 전체 유저에 대해 예측할 수 있습니다.

딥마인드에서 개발된 Protein Foldling 문제해결을 위한 AlphaFold가 Node Level 접근의 다른 예시입니다. 단백질 속에 있는 Amino acid들이 Node, Node 사이의 가까움 정도를 Edge로 표현합니다. 그리고 각 Node의 새로운 Position를 예측하고 이를 이용해 3D형태의 단백질 구조를 예측합니다.

표준 Supervised Learning과의 차이점이 있습니다. 가장 중요한 차이점은 Graph의 Node들이 서로 독립이 아니라는 점입니다. iid Set을 가정하고 모델링 하는 대신 Node들 사이의 상호연결을 모델링합니다. 또 다른 차이점은 모델을 학습할 때 Label되지 않은 Test Node들을 사용해 Semi-supervised로 여길 수 있습니다. 하지만 기존 Semi-supervised도 각 Sample에 대해 iid 가정을 하기 때문에 차이가 있습니다.

1.2.2 Relation Prediction

Edge Level의 한 종류로 Relation Prediction이 있습니다. Relation Prediction은 누락된 Relationship 정보를 예측하는 것입니다. 다른 말로 Link Prediction, Graph Completion, Relational Inference로 불리기도 합니다. 우리가 일부 단백질 사이의 관계만을 알고 있을 떄, 누락된 관계를 예측할 때 사용할 수 있습니다. 추가로, 친구들 사이의 Friendship “정도” 예측으로 접근할 수 있고, 약들 사이의 부작용 중 구토, 섩사, 고열 중 “어디에 속하는지” 예측하는 것으로 접근할 수 있습니다.

1.2.3 Clustering and Community Detection

Clustering and Community Detection은 Subgraph Level의 Unsupervised Clustering 방법입니다. 한 개의 입력 Graph \(G = (N, E)\)가 주어졌을 때, 내부에서 여러 Subgraph로 클러스터링합니다. 유전 작용 네트워크에서 기능별 모듈로 분류하거나, 금융 네트워크에서 사기 단체를 찾아내는 것을 예로 들 수 있습니다.

또 다른 Subgraph Level예시로, Traffic Predition이 있습니다. 전체 교통상황 중 일부인 출발지부터 목적지까지를 하나의 Subgraph로 여길 수 있습니다. 이때 목적지까지 도착하는데 걸리는 시간 ETA를 예측하는 Task입니다.

1.2.4 Graph Classification, Regression, and Clustering

하나의 Graph 안에서 각각의 Component에 대해 예측하는 대신 각각의 Graph에 대해서 독립적으로 예측하는 Graph Level이 있습니다. Graph Classification과 Regression은 하나의 Graph에 대해 목표값을 예측합니다. Graph Clustering은 Graph 쌍 사이의 유사도를 계산해 Grouping합니다. Graph Level에서는 각 Graph를 독립적으로 보기 때문에 표준 ML과 더 유사하다고 할 수 있습니다.