[CS224W GraphML] 2-1. Graph 통계량: networkx, Centrality, Graphlet

Graph Representation Learning Book의 Chapter2을 번역, 요약, 정리했습니다. 내용에 맞춰 파이썬 패키지 networkx 사용 예시를 추가했습니다.

Graph Representation Learning과 Deep Learning을 소개하기 전에, 이후 장들의 기초가 되는 배경지식과 고전적인 Graph ML 방법을 소개합니다.

Node와 Graph 분류 문제에 사용할 수 있는 기초 그패트 통계과 Kernel 방법을 먼저 다룹니다. 이후 이웃 Node 사이에 얼만큼 Overlap 겹치는지 나타는 방법을 다루고, 마지막으로 Graph Community Detection 방법으로 유명한 Spectal Clustering을 소개하겠습니다.

2.1 Graph Statistics and Kernel Methods

Machine Learning의 입력으로 사용되는 통계량과 Feature가 필요합니다. Node Level에서 보편적으로 사용하는 통계량에 대해 소개합니다.

2.1.1 Node-level Statistics and Features

Logistic Regression과 같은 Node 분류 모델에 사용될 수있는 통계값과 속성들이 있습니다. 이런 속성값들은 Node들을 구분짓는 값들로 고려돼야 합니다.

2.1.1.1 Node Degree

Node Degree는 하나의 Node를 지나는 Edge의 개수로 자유도라 불리는 가장 명확 값입니다. Node-level ML task에서 가장 의미있는 속성값 중 하나입니다.

\(u \in V\)의 자유도는 \(d_u\)로 표현합니다. 이전 장에서 설명한 인접 행렬에서 \(u\)에 대한 하나의 열 또는 행의 합산과 같습니다. (Undirected Graph 기준)

\[d_u = \sum_{v \in V}A[u, v]\]

에를 들어, 아래 Graph에서 Node A의 자유도는 2 입니다.

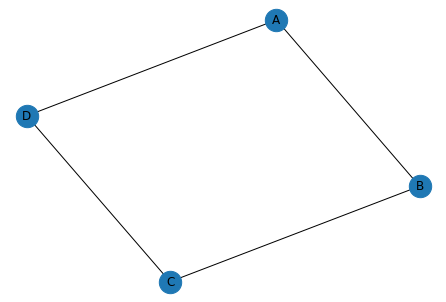
아래와 같은 파이썬 코드로도 확인 할 수 있습니다.

import networkx as nx
import numpy as np

adjacency = np.array([
    [0, 1, 0, 1],
    [1, 0, 1, 0],
    [0, 1, 0, 1],
    [1, 0, 1, 0],
])

labels={0: "A", 1: "B", 2: "C", 3: "D"}

G = nx.Graph(adjacency)  # matrix로 Undirected Graph 정의
G = nx.relabel_nodes(G, labels)  # Node 이름 변경
G.degree()
# >>> DegreeView({'A': 2, 'B': 2, 'C': 2, 'D': 2})

2.1.1.2 Node Centrality

Node 자유도는 단순해 표현하기 좋지만 Graph 내에서 Node의 중요도 Importance를 표현하기에는 부족합니다. Node Centrality 중심성으로 알려진 속성값을 고려해야합니다.

Eigenvector Centrality
Betweenness Centrality
Closeness Centrality

가장 많이 알려진 Eigenvector Centrality가 있습니다. Node 주변에 있는 이웃 Node들의 중요도를 이용해 표현합니다. Node \(v\)의 Eigenvector Centrality는 \(e_v\)로 표현하고, 이웃 Node들의 평균 Centrality입니다. 이웃 Node의 Centrality가 클 경우, 해당 Node의 Centrality도 커지게 됩니다.

\[e_u = \frac{1}{\lambda} \sum_{v \in V} A [u, e]e_v \forall u \in V.\]

\(\lambda\) 는 하나의 상수값입니다. 모든 Node의 Centrality 벡터 \(e\)는 아래 처럼 행령식으로 표현할 수 있습니다. 행렬식으로 표현할 경우 Centrality는 \(A\)의 고유벡터 Eigenvector임을 알 수 있습니다. 가장 큰 고유값 Eigenvalue \(\lambda_{\text{max}}\) 에 해당하는 Eigenvector \(e_{\text{max}}\)를 이용해 Centrality 를 표현합니다.

\[\lambda e = A e.\]

nx.eigenvector_centrality(G)
# >>> {'A': 0.5, 'B': 0.5, 'C': 0.5, 'D': 0.5}

Betweenness Centrality는 다른 Node들의 최단 경로에 많이 속할 수록 중요함을 나타냅니다.

\[c_v = \sum_{s \neq v \neq t} \frac{\text{# shorted paths between s and t that contain v}}{\text{# shorted paths between s and t}}\]

아래 [Graph1]에서 Node A에 대해서 계산해보겠습니다. A외에 Node는 B, C, D가 있습니다. B-C 사이에 최단 경로는 B-C 하나이고 이중에 A를 지나는 경우는 없어 0입니다. 마찬가지로 C-D 사이에 최단 경로는 C-D 하나이고 이중에 A를 지나는 경우는 없어 0입니다. B-D 사이에 최단 경로는 B-A-C 와 B-C-D 두 개이고 이중에 A를 지나는 경우는 하나로 1/2 입니다. 이 3가지 경우의 합산인 0.5가 A Node의 Betweenness Centrality가 됩니다.

nx.betweenness_centrality(G, normalized=False)
# >>> {'A': 0.5, 'B': 0.5, 'C': 0.5, 'D': 0.5}

Closeness Centrality는 모든 Node까지의 최단 거리가 짧을 수록 중요함을 나타냅니다. 아래 수식의 분자는 CS224W에서는 1로 되어 있습니다. networkx의 결과와 맞추기 위해 “총 Node 수(n) - 1”로 표현했습니다. 참고

\[c_v = \frac{n - 1}{\sum_{u \neq v} \text{shortest path length between u and v}}\]

위 [Graph1]에서 Node A에 대해서 계산해보겠습니다. A-B 까지 최단거리 1, A-C 까지 최단 거리 2, A-D 까지 최단 거리 1로 모든 Node에 대한 최단거리 합은 총합 4입니다. 최종 Closeness Centrality 3/4입니다.

nx.closeness_centrality(G)
# >>> {'A': 0.75, 'B': 0.75, 'C': 0.75, 'D': 0.75}

2.1.1.3 Clustering Coefficient

앞의 두 지표는 Node 주변의 Local Structure를 나타내기에는 부족합니다. 예를 들어, 아래 [Graph2]에서 Node \(v\)는 모두 4개의 다른 Node와 연결되어 있습니다. 하지만 연결된 Node 사이에서 연결된 정도가 다릅니다. 이웃 Node가 서로서로 모두 이웃 Node 일때 Clustering Coefficient는 1이 됩니다.

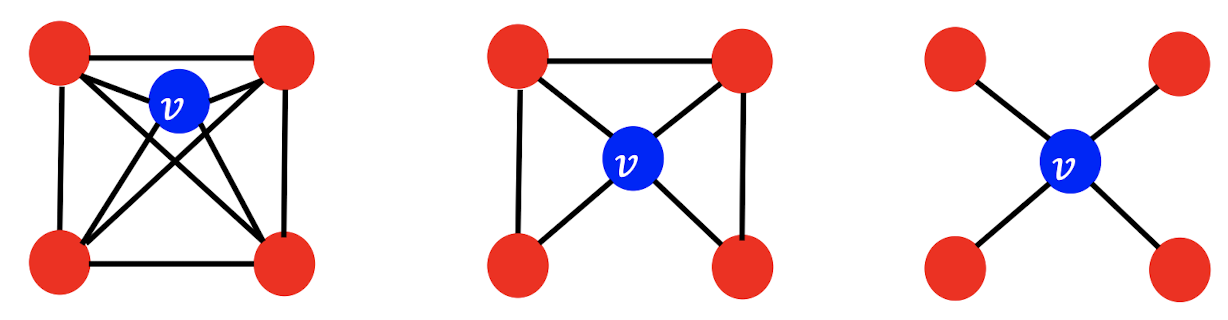
아래 수식에서 \(N(u) = \{v \in V: (u,v)\in E\}\)는 Node \(u\)의 이웃 Node Set을 나타냅니다. 아웃 Node들의 전체 연경 경우의 수 대시 실제 연결된 개수를 의미합니다.

\[c_v = \frac{|(v_1,v_2) \in E: v_1, v_2 \in N(u)|}{d_v \choose 2}\]

아래 [Graph1]은 모든 Node에 대해 이웃 Node끼리 연결되지 않아 0을 갖습니다.

nx.clustering(G)
# >>> {'A': 0, 'B': 0, 'C': 0, 'D': 0}

2.1.1.4 Closed triangles, ego graphs, and motifs.

Clustering Coefficient 를 보는 또 다른 방법은 각 Node의 Local Neighborhood안에 있는 닫힌 삼각관계의 개수를 보는 것 입니다. Node의 Local Neighborhood는 Ego Graph라고 하기도 합니다. 1-Hop Network로 한 층의 Edge로만 연결된 부분 Graph입니다. 닫힌 삼각관계란 Social Network에서 나의 친구가 있고, 친구의 친구가 나와도 친구인 상황입니다.

nx.triangles(G)

삼각관계를 더 일반적으로 표현하면 Graphlet또는 Motifs라고 합니다. 다르게 연결된 Subgraph들로 5개의 Node 연결 종류는 [그림2]와 같습니다.

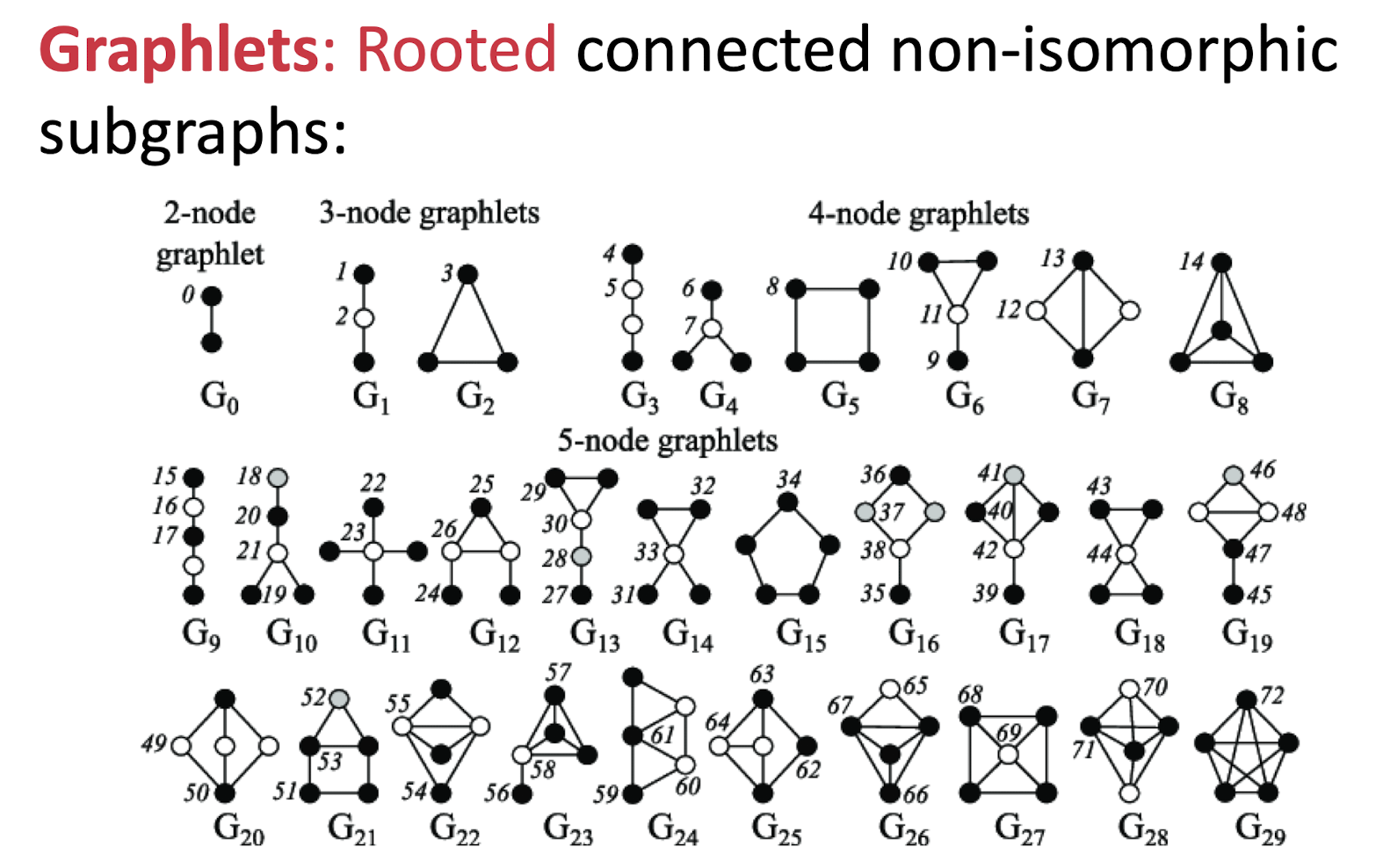
Node가 각 Graphlet에 해당하는 경우의 수를 나열한 벡터인 Graphlet Degree Vector(GDV)로도 표현될 수 있습니다.

이를 좀더 확장하면 Graph Level에서 더 표현하는 방법으로 사용 될 수 있습니다.

Degree: 연결된 Edge의 개수
Clustering Coefficient: 연결된 삼각관계의 개수
GDV: 각 Graphlet의 개수 벡터

2.1.2 Graph-level Features and Graph Kernels

이번에는 하나의 Graph에 대해서 Feature를 추출하는 방식을 소개하겠습니다. Graph Level에서는 Feature Vector 대신 Graph Kernel Method를 주로 사용합니가.

2.1.2.1 Bag of Nodes

가장 간단한 벙법은 Node Level의 통게값을 Aggregation 통합하는 것입니다. 단순히 전체 노도의 개수로 표현할 수 있고, (자유도가 1인 Node의 개수, 2인 Node의 개수, 3인 Node의 개수,,,)처럼 벡터로 표현할 수 있습니다.

이 방법은 Node Level의 Local 정보만 반영해서 만들어지기 때문엔 Grobal 속성 정보는 놓치기 쉽습니다.

2.1.2.2 The Weisfeiler-Lehman Kernel

Bag of Nodes을 이웃 정보를 반복적으로 통합하는 방식으로 발전시켜 사용할 수 있습니다. Ego Graph의 좁은 영역보다 많은 정보를 갖는 Node Level Feature를 발전시켜 Graph Level Feature로 사용합니다.

각 Node의 초기 레이블 \(l^{(0)}(v)\)을 설정합니다. 단순히 \(l^{(0)}(v) = d_v \forall v \in V\) 와 같이 자유도로 할당할 수 있습니다.
새로운 레이블은 이웃 Node의 현재 레이블을 이용해 표현합니다. 이때 현레 레이블 집합으로 Hashing한 새로운 값을 사용합니다. \(l^{(i)}(v) = HASH(\{\{ l^{(i-1)}(u) \forall u \in N(v) \}\})\)
Step 2를 K번 반복헤 \(l^{(K)}(v)\)를 할당합니다.

이때 K는 상황에 맞게 직접 설정합니다. \(l^{(K)}(v)\)는 K-hop(K 거리 만큼 떨어진) 이웃 정보를 요약하게 됩니다. 최종 레이블 값의 분포나 요양 정보를 통해 Graph를 표현하는 데 사용할 수 있습니다. Weisfeiler-Lehman Kernel을 이용해 두개의 Graph에 대해 각각 표현하고, 표현 정보를 이용해 두 Graph의 유사도를 측정할 수 있습니다.

[Graph2]에 대해 1, 2과정을 구체적으로 예시를 들어 보겠습니다. (2, 3, 2)와 (3, 3)은 각각 새로운 값인 4와 5로 할당해주는 과정이 Hashing과정입니다.

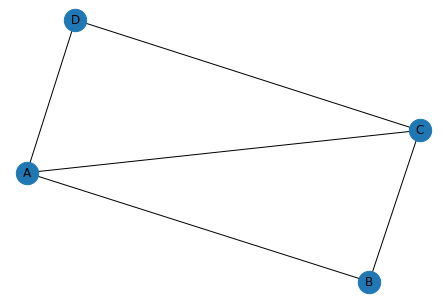
\[l^{(0)}(A) = 3, l^{(0)}(B) = 2, l^{(0)}(C) = 3, l^{(0)}(D) = 2\]

\[\begin{align} l^{(1)}(A) &= (l^{(0)}(B), l^{(0)}(C), l^{(0)}(D)) = (2, 3, 2) = 4 \\ l^{(1)}(B) &= (l^{(0)}(A), l^{(0)}(C)) = (3, 3) = 5 \\ l^{(1)}(C) &= (l^{(0)}(A), l^{(0)}(B), l^{(0)}(D)) = (3, 2, 2) = 4 \\ l^{(1)}(D) &= (l^{(0)}(A), l^{(0)}(C)) = (3, 3) = 5 \\ \end{align}\]

[Graph2]에 대한 K 1 Weisfeiler-Lehman Kernel의 결과를 WLKernel-1([Graph2]) = (1:0, 2:2, 3:2, 4:2, 5:2) 처럼 표현할 수 있습니다.

2.1.2.3 Graphtlets and Path-based Methods

Node Level을 넘어 Graph Level에서도 Graphlet이라 불리는 Subgraph들의 개수를 이용해 Feature를 만들 수 있습니다. 하나의 Full Graph 안에 각각의 Graphlet이 속한 개수를 이용합니다. 히지만 이 방법은 계산하기 어렵다는 문제가 있어 대략적으로 근사시키는 방법이 사용되기도 합니다.

모든 Graphlet을 세는 대신 Path-based Method를 사용할 수 있습니다. Graph에서 발생할수 있는 경로의 종류로 단순화한 방법입니다. Random Walk Kernel과 Shortest Path Kernel이 이에 속합니다. 해당 방법에 대해서는 3장에서 구체적으로 다룰 예정입니다.