Graph Representation Learning Book의 Chapter2을 번역, 요약, 정리했습니다.
2.1 Graph 통계량에 이어서 이후 장들의 기초가 되는 배경지식과 고전적인 Graph ML 방법을 소개합니다.
2.2 Neighborhood Overlap Detection
Graph Statistics에서 각 Node / Graph의 Feature 추출을 다루었습니다. 해당 Feature들은 많은 Classification 문제들에 유용합니다. 하지만 Node들 사이의 관계를 나타내기에는 부족해 두 Node 사이에 Edge 유무를 예측하는 Relation Prediction 등의 Task에는 부적절합니다.
이번장에서는 Node 쌍이 연관성을 정량적으로 나타내는 이웃유사도 Neighborhood Overlap과 관련된 통계값을 다루겠습니다.
가장 단순히 두 Node가 공유하는 이웃 Node 수로 판단할 수 있습니다. \(N(u)\)는 Node u의 이웃 Node 집합을 의미합니다. 이때 \(S \in R^{|V| \times |V|}\) 는 Pairwise Node 통계량을 요약하는 Similarity Matrix라고 합니다. \(Edge(u, v)\)의 가능도는 \(S[u,v]\)에 비례합니다.
\[S[u,v] = |N(u) \cap N(v)|\]ML 문제로 Setting하는 과정은 다음과 같습니다. 학습 시에 전체 Edge 셋의 일부만 알고 있다고 가정해 학습합니다. 나머지 보지않은 Edge를 이용해 모델의 성능을 평가합니다.
2.2.1 Local Overlap Measures
Local Overlap은 단순히 두 Node의 공통 이웃 Node 수를 이용합니다. 정규화 과정을 통해 자유도가 큰 Node에 편향을 줄여주는 것이 필요합니다.
Sorensen Index
Sorensen Index는 각 Node의 자유도의 합으로 나눠 정규화할 수 있습니다.
\[S_{Sorensen}[u,v] = \frac{2|N(u) \cap N(v)|}{d_u + d_v} \in R^{|V| \times |V|}\]Salton Index
Salton Index는 각 Node의 자유도의 곱으로 정규화 합니다. 두 Node가 모두 같은 Node만을 이웃으로 가질 경우 Similarity는 1이 됩니다.
\[S_{Salton}[u,v] = \frac{2|N(u) \cap N(v)|}{\sqrt{d_u d_v}} \in R^{|V| \times |V|}\]Jaccard Overlap
Jaccard Overlap은 두 Node의 이웃 Node 합집합의 수로 나눠줍니다.
\[S_{Jaccard}[u,v] = \frac{|N(u) \cap N(v)|}{|N(u) \cup N(v)|} \in R^{|V| \times |V|}\]Resource Allocation Index
앞의 Index들은 대상이 되는 Node의 자유도로 인한 편향을 줄였습니다. 공유하는 공통 이웃 Node의 Inportance도 고려해야합니다. 예를 들어, Social Network에서 A와 B가 공통적으로 연에인을 팔로우하고, A와 다른 C는 일반인 D를 같이 팔로우 하는 경우를 생각해 보겠습니다. A와 B일 가능성보다 A와 C가 친구일 가능성이 더 높다고 볼 수 있습니다. 이처럼 자유도가 클 수록 낮은 중요도를 반영하는 것이 Resource Allocation Index 입니다.
보편적인 정보들보다 특별한 한가지 정보가 더 강력할 수 있습니다.
\[S_{RA}[v_1,v_2] = \sum_{u \in N(v_1) \cap N(v_2)} \frac{1}{d_u}\]Adamin-Adar Index
log를 취해서 반영할 수도 있습니다.
\[S_{AA}[v_1,v_2] = \sum_{u \in N(v_1) \cap N(v_2)} \frac{1}{log(d_u)}\]2.2.2 Global Overlap Measures
Local Overlap은 매우 효과적인 통계량입니다. 하지만, Local Overlap은 오직 주변 Node의 이웃만 고려한다는 제약이 있습니다. 예를 들어, 아래 [Graph1]에서 Node A와 Node F는 꽤 연결성이 높아 보이지만 앞의 Local Overlap은 0ㅇ이됩니다. 이런 상황을 반영하기 위한 Global Overlap 통계량을 소개합니다.
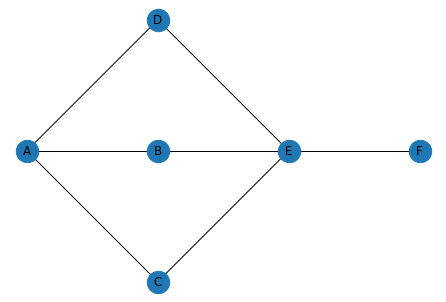
Katz Index
Katz Index는 가장 기본 Global Overlap Measures 입니다. 단순히 두 Node 사이를 연결하는 모든 길이의 경로의 개수를 계산합니다. 예를 들어, [Graph1]에서 Node A와 F를 생각해 보겠습니다.
- 길이가 1인 경로: 0
- 길이가 2인 경로: 0
- 길이가 3인 경로: 3 (A-D-E-F, A-B-E-F, A-C-E-F)
- 길이가 4인 경로: 0
위 과정을 길이가 0 부터 무한대까지 모두 계산합니다. Node u와 v사이의 거리가 l 인 경로의 수는 Graph의 인접행렬 A의 l 제곱 행렬 \(A^{l}\)의 \([u, v]\)와 동일합니다. (관련한 증명 또는 구체적인 설명은 이후에 추가하겠습니다.)
Katz Index는 다음과 같이 표현할 수 있습니다. 이때 \(\beta\)는 양의 실수입니다. 1보다 작은 숫자일 경우 경로의 길이가 길어질 수록 중요도를 낮춤을 의미합니다.
\[S_{Katz}[u, v] = \sum_{i=1}^{\infty}\beta^{i}A^{i}[u,v]\]위 무한까지의 합산 과정을 등비급수 수식을 빌려와 정리하면 다음과 같습니다.
\[S_{Katz}[u, v] = (I - \beta A)^{-1} - I \in R^{|V| \times |V|}\]import numpy as np
beta = 0.9
A = np.array([
[0, 1, 1, 1, 0, 0],
[1, 0, 0, 0, 1, 0],
[1, 0, 0, 0, 1, 0],
[1, 0, 0, 0, 1, 0],
[0, 1, 1, 1, 0, 1],
[0, 0, 0, 0, 1, 0],
])
I = np.identity(A.shape[0])
np.linalg.inv(I - beta * A) - I